上一篇我们介绍了使用WebGL的基础,包括顶点着色器、片元着色器、初始化WebGL,初始化着色器以及变换、动画、颜色、纹理等,这一部分的内容我们就来进入三维的世界。和上一篇文章一样,我们的这篇只做个大概的介绍,详细的内容部分请参阅《WebGL编程指南》一书。
代码存储在我的GitHub中。
首先我们来绘制一个三维的实例。
示例程序:https://zrysmt.github.io/demo/webgl-demo/demo/10-HelloCube.html.

实例的源码程序:https://github.com/zrysmt/data-viz/blob/master/webgl/demo/HelloCube.js
其实这里我们应该注意到示例和源码的结构对应,下面的一些我可能只给出一个url地址。
1.视图、投影和索引矩阵
从main函数开始
1 | function main() { |
顶点着色器和片元着色器
和上一篇有一些的不同1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'uniform mat4 u_MvpMatrix;\n' + //模型矩阵,设置视图/投影
'varying vec4 v_Color;\n' + //传值给片元着色器
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
' v_Color = a_Color;\n' +
'}\n';
// Fragment shader program
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' + //精度限定 中等精度
'#endif\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_FragColor = v_Color;\n' +
'}\n';
关于attribute uniform varying
attribute:只能是全局的,只能出现在顶点着色器,标识逐顶点信息;
uniform:只能是全局的,可以在顶点着色器和片元着色器上,如果两个地方均定义,那么这变量被两个着色器共享了;
varying:只能是全局的,负责从顶点着色器向片元着色器传输数据。
视图矩阵(view matrix)
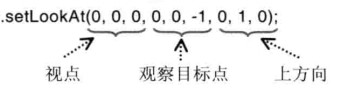
视点、观察点和上方向决定视图矩阵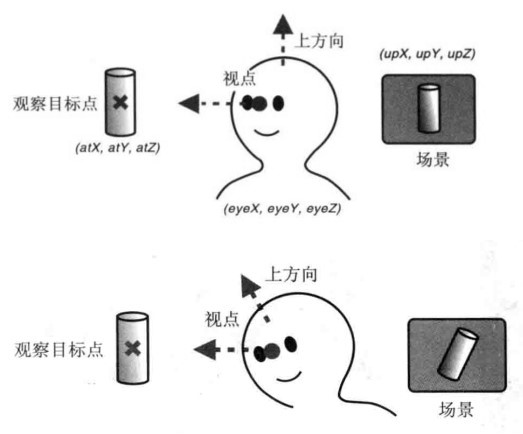
1
2var mvpMatrix = new Matrix4();
mvpMatrix.setLookAt(3, 3, 7, 0, 0, 0, 0, 1, 0)
投影矩阵
投影的作用就是使得距离近的看的比较大,距离远的看的比较小
示例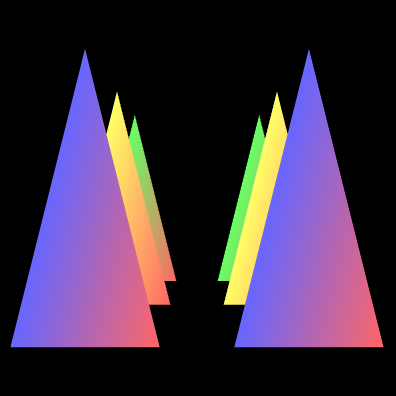
1
projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);

三角形与可视空间的位置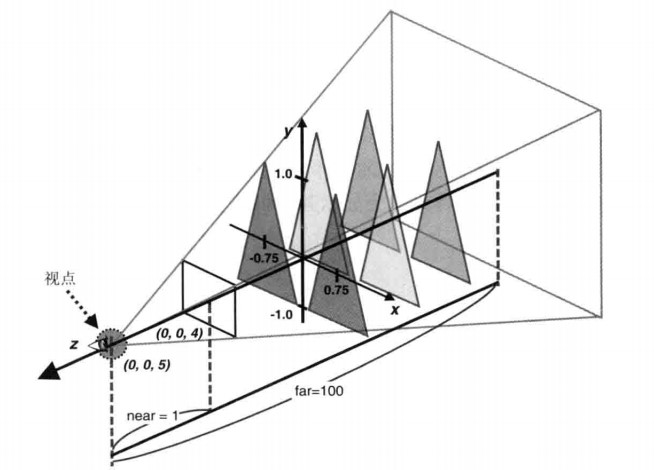
其实投影矩阵的核心就是两种变换,1)按比例缩放;2)平移
消除被遮挡的面
1 | gl.enable(gl.DEPTH_TEST); |
清除颜色和深度buffer1
2// Clear color and depth buffer
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
重要的公式
我们总结下一个重要的公式,WebGL绘制物体的位置为:1
<投影矩阵> X <视图矩阵> X <模型矩阵> X <顶点坐标>
绘制立方体
1 | function initVertexBuffers(gl) { |
立方体的结构1
2
3
4
5
6
7 v6----- v5
/| /|
v1------v0|
| | | |
| |v7---|-|v4
|/ |/
v2------v3
首先顶点坐标和顶点坐标的颜色存储在verticesColors矩阵中。
而WebGL的绘制是按照三角形的形式一个一个绘制的,那么意味着一个立方体的一个面有两个三角形,一个立方体总共需要26 = 12个三角形,一个三角形需要3个顶点,那么一共需要绘制 312 = 36个顶点。我们知道一个立方体只需要8个顶点就可以了。为此我们在这里使用了索引矩阵(indices),索引矩阵也要写入缓存中。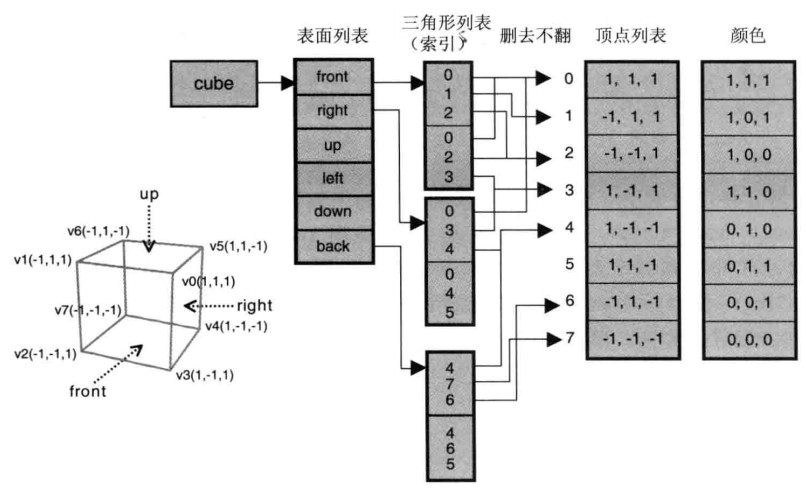
这样我们就能完成绘制了1
gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
注意这里的n = indices.length。
2.光照
我们主要关注下面三种形式的光照:
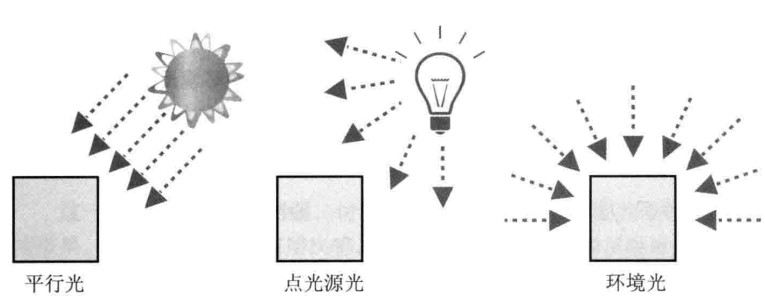
物理表面反射光线:分为漫反射和环境反射
环境反射
1 | <环境反射光颜色> = <入射光颜色> X <表面基底色> |
平行光下的漫反射
1 | <漫反射光颜色> = <入射光颜色> X <表面基底色> X cosθ |
即:1
<漫反射光颜色> = <入射光颜色> X <表面基底色> X (<光线方向> · <法线方向>)
我们只用漫反射的效果的时候
示例
由于只考虑漫反射,右边的部分几乎是黑色了,这时候我们来考虑下环境光。
环境反射下的表面的反射光颜色1
<表面的反射光颜色> = <漫反射颜色> + <环境反射光颜色>
示例
我们来看下着色器源码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' + //表面颜色
'attribute vec4 a_Normal;\n' + // 表面法向量
'uniform mat4 u_MvpMatrix;\n' +
'uniform vec3 u_DiffuseLight;\n' + // 漫反射光颜色
'uniform vec3 u_LightDirection;\n' + // 漫反射入射光方向 (in the world coordinate, normalized)归一化后
'uniform vec3 u_AmbientLight;\n' + // 环境光颜色
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
// 归一化方向量
' vec3 normal = normalize(a_Normal.xyz);\n' +
// <归一化的光线方向> 点乘 <归一化法线向量>
' float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
// 计算漫反射颜色
' vec3 diffuse = u_DiffuseLight * a_Color.rgb * nDotL;\n' +
// 计算环境光颜色
' vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
// 两者相加得到物体最终的颜色
' v_Color = vec4(diffuse + ambient, a_Color.a);\n' +
'}\n';
// Fragment shader program
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' +
'#endif\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_FragColor = v_Color;\n' +
'}\n';
对于变化后的物体,物体的法向量也会改变
示例1
<变换后的法向量> = <法向量> X <变化矩阵的逆转置矩阵>
1 | normalMatrix.setInverseOf(modelMatrix); |
在顶点着色器中变化原法向量1
vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal))
最后我们来看下最终的漫反射光颜色的公式
1
<漫反射光颜色> = <入射光颜色> X <表面基底色> X (<光线方向> ·(<模型矩阵逆转置矩阵> X <法线方向>))
点光源
1 | 光线方向 = 归一化(点光源方向 - 顶点坐标) |
1 | // 顶点处的光线方向 = 点光源的光坐标 - 顶点坐标 |
3.层次模型
有的物体的运动会带动别的物体,如上臂的运动会带动下臂和手掌的运动。
示例:https://zrysmt.github.io/demo/webgl-demo/ch09/JointModel.html
示例源码:https://github.com/zrysmt/data-viz/blob/master/webgl/ch09/JointModel.js

下边的(Arm1)会带动上边的(Arm2)运动,而上边的运动不会带动下边的。
思路:共用一个变换的模型矩阵:g_modelMatrix,Arm1变化g_modelMatrix也会变化,那么Arm2也会使用这个模型。谁能控制谁,关键是谁先写上去,谁后写上去,先写上去的控制后写上去的。1
2
3
4
5
6
7
8
9
10// Arm1
var arm1Length = 10.0; // Length of arm1
g_modelMatrix.setTranslate(0.0, -12.0, 0.0);
g_modelMatrix.rotate(g_arm1Angle, 0.0, 1.0, 0.0); // Rotate around the y-axis
drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // Draw |
// Arm2
g_modelMatrix.translate(0.0, arm1Length, 0.0); // Move to joint1
g_modelMatrix.rotate(g_joint1Angle, 0.0, 0.0, 1.0); // Rotate around the z-axis
g_modelMatrix.scale(1.3, 1.0, 1.3); // Make it a little thicker
drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // Draw